Dof of a Rigid Body

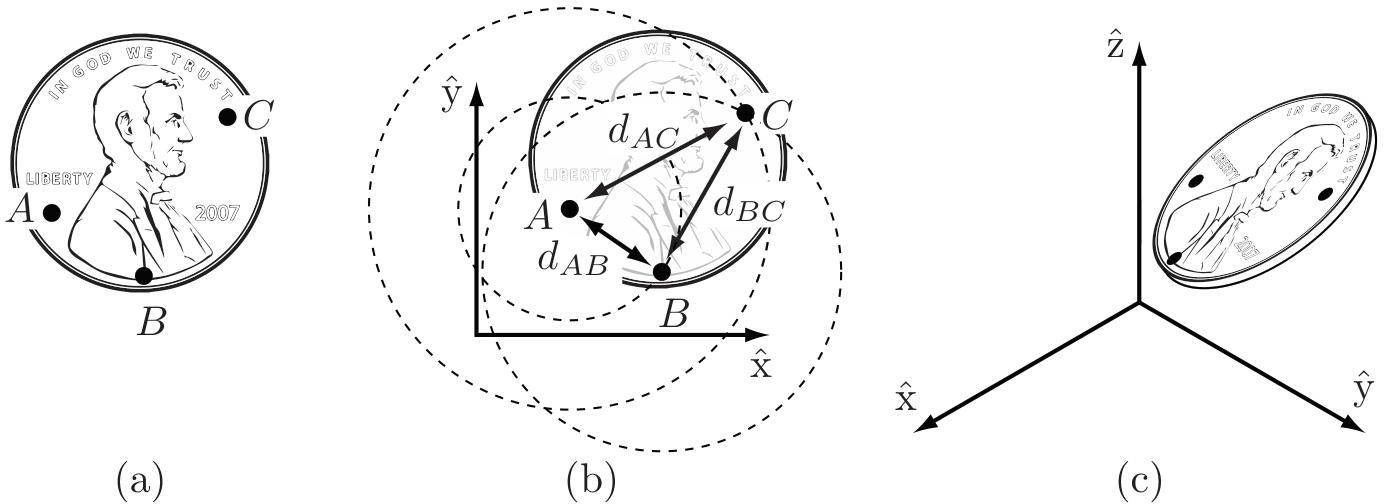
Figure 2.2:

(a) Choosing three points fixed to the coin.
(b) Once the location of $A$ is chosen, $B$ must lie on a circle of radius $d_{A B}$ centered at $A$ . Once the location of $B$ is chosen, $C$ must lie at the intersection of circles centered at $A$ and $B$ . Only one of these two intersections corresponds to the “heads up” configuration.
(c) The configuration of a coin in three-dimensional space is given by the three coordinates of $A$ , two angles to the point $B$ on the sphere of radius $d_{A B}$ centered at $A$ , and one angle to the point $C$ on the circle defined by the intersection of the a sphere centered at $A$ and a sphere centered at $B$ .

Continuing with the example of the coin lying on the table, choose three points $A$ , $B$ , and $C$ on the coin (Figure 2.2 (a)). Once a coordinate frame $\hat{x} - \hat{y}$ is attached to the plane, the positions of these points in the plane are written $(x_{A}, y_{A})$ $(x_{B}, y_{B})$ ,and $(x_{C}, y_{C})$ . If the points could be placed independently anywhere in the plane, the coin would have six degrees of freedom - two for each of the three points. But, according to the definition of a rigid body, the distance between point $A$ and point $B$ , denoted $d (A, B)$ , is always constant regardless of where the coin is. Similarly, the distances $d (B, C)$ and $d (A, C)$ must be constant. The following equality constraints on the coordinates $(x_{A}, y_{A})$ $(x_{B}, y_{B})$ ,and $(x_{C}, y_{C})$ must therefore always be satisfied:

\begin{array}{r} d (A, B) = \sqrt{(x_{A} - x_{B})^{2} + (y_{A} - y_{B})^{2}} = d_{A B} \\ d (B, C) = \sqrt{(x_{B} - x_{C})^{2} + (y_{B} - y_{C})^{2}} = d_{B C} \\ d (A, C) = \sqrt{(x_{A} - x_{C})^{2} + (y_{A} - y_{C})^{2}} = d_{A C} . \end{array}

To determine the number of degrees of freedom of the coin on the table, first choose the position of point $A$ in the plane (Figure 2.2 (b)). We may choose it to be anything we want, so we have two degrees of freedom to specify, namely $(x_{A}, y_{A})$ .

Once $(x_{A}, y_{A})$ is specified, the constraint $d (A, B) = d_{A B}$ restricts the choice of $(x_{B}, y_{B})$ to those points on the circle of radius $d_{A B}$ centered at $A$ . A point on this circle can be specified by a single parameter, e.g., the angle specifying the location of $B$ on the circle centered at $A$ . Let's call this angle $ϕ_{A B}$ and define it to be the angle that the vector $\vec{A B}$ makes with the $\hat{x}$ - axis.

Once we have chosen the location of point $B$ , there are only two possible locations for $C$ : at the intersections of the circle of radius $d_{A C}$ centered at $A$ and the circle of radius $d_{B C}$ centered at $B$ (Figure 2.2 (b)). These two solutions correspond to heads or tails.

In other words, once we have placed $A$ and $B$ and chosen heads or tails, the two constraints $d (A, C) = d_{A C}$ and $d (B, C) = d_{B C}$ eliminate the two apparent freedoms provided by $(x_{C}, y_{C})$ , and the location of $C$ is fixed. The coin has exactly three degrees of freedom in the plane, which can be specified by $(x_{A}, y_{A}, ϕ_{A B})$ .

Suppose that we choose to specify the position of an additional point $D$ on the coin. This introduces three additional constraints: $d (A, D) = d_{A D}$ , $d (B, D) = d_{B D}$ , and $d (C, D) = d_{C D}$ . One of these constraints is redundant 冗余的 , i.e., it provides no new information; only two of the three constraints are independent. The two freedoms apparently introduced by the coordinates $(x_{D}, y_{D})$ are then immediately eliminated by these two independent constraints. The same would hold for any other newly chosen point on the coin, so that there is no need to consider additional points.

We have been applying the following general rule for determining the number of degrees of freedom of a system:

degrees of freedom = (sum of freedoms of the points) - (number of independent constraints) (2.1)

This rule can also be expressed in terms of the number of variables and independent equations that describe the system:

\begin{array}{r} degrees of freedom = (number of variables) - \\ (number of independent equations) . \end{array} (2.2)

This general rule can also be used to determine the number of freedoms of a rigid body in three dimensions. For example, assume our coin is no longer confined to the table (Figure 2.2 (c)). The coordinates for the three points $A, B$ , and $C$ are now given by $(x_{A}, y_{A}, z_{A})$ , $(x_{B}, y_{B}, z_{B})$ , and $(x_{C}, y_{C}, z_{C})$ , respectively.

Point $A$ can be placed freely (three degrees of freedom).
The location of point $B$ is subject to the constraint $d (A, B) = d_{A B}$ , meaning it must lie on the sphere of radius $d_{A B}$ centered at $A$ . Thus we have $3 - 1 = 2$ freedoms to specify, which can be expressed as the latitude and longitude for the point on the sphere.
Finally, the location of point $C$ must lie at the intersection of spheres centered at $A$ and $B$ of radius $d_{A C}$ and $d_{B C}$ , respectively. In the general case the intersection of two spheres is a circle, and the location of point $C$ can be described by an angle that parametrizes this circle. Point $C$ therefore adds $3 - 2 = 1$ freedom.
Once the position of point $C$ is chosen, the coin is fixed in space.

In summary, a rigid body in three- dimensional space has six freedoms, which can be described by

the three coordinates parametrizing point $A$ ,
the two angles parametrizing point $B$ ,
and one angle parametrizing point $C$ , provided $A$ , $B$ , and $C$ are noncollinear 非共线的.
Other representations for the configuration of a rigid body are discussed in Chapter 3.

We have just established that

a rigid body moving in three- dimensional space, which we call a spatial rigid body, has six degrees of freedom.
Similarly, a rigid body moving in a two- dimensional plane, which we henceforth call a planar rigid body, has three degrees of freedom. (This latter result can also be obtained by considering the planar rigid body to be a spatial rigid body with six degrees of freedom but with the three independent constraints $z_{A} = z_{B} = z_{C} = 0$ . )

Since our robots consist of rigid bodies, Equation (2.1) can be expressed as follows:

\begin{aligned} degrees of freedom & = (sum of freedoms of the bodies) - \\ (number of independent constraints) . \end{aligned}, (2.3)

Equation (2.3) forms the basis for determining the degrees of freedom of general robots, which is the topic of the next section.